10216 Count Circle Groups
문제
난이도 : G4
알고리즘 : 분리집합
풀이
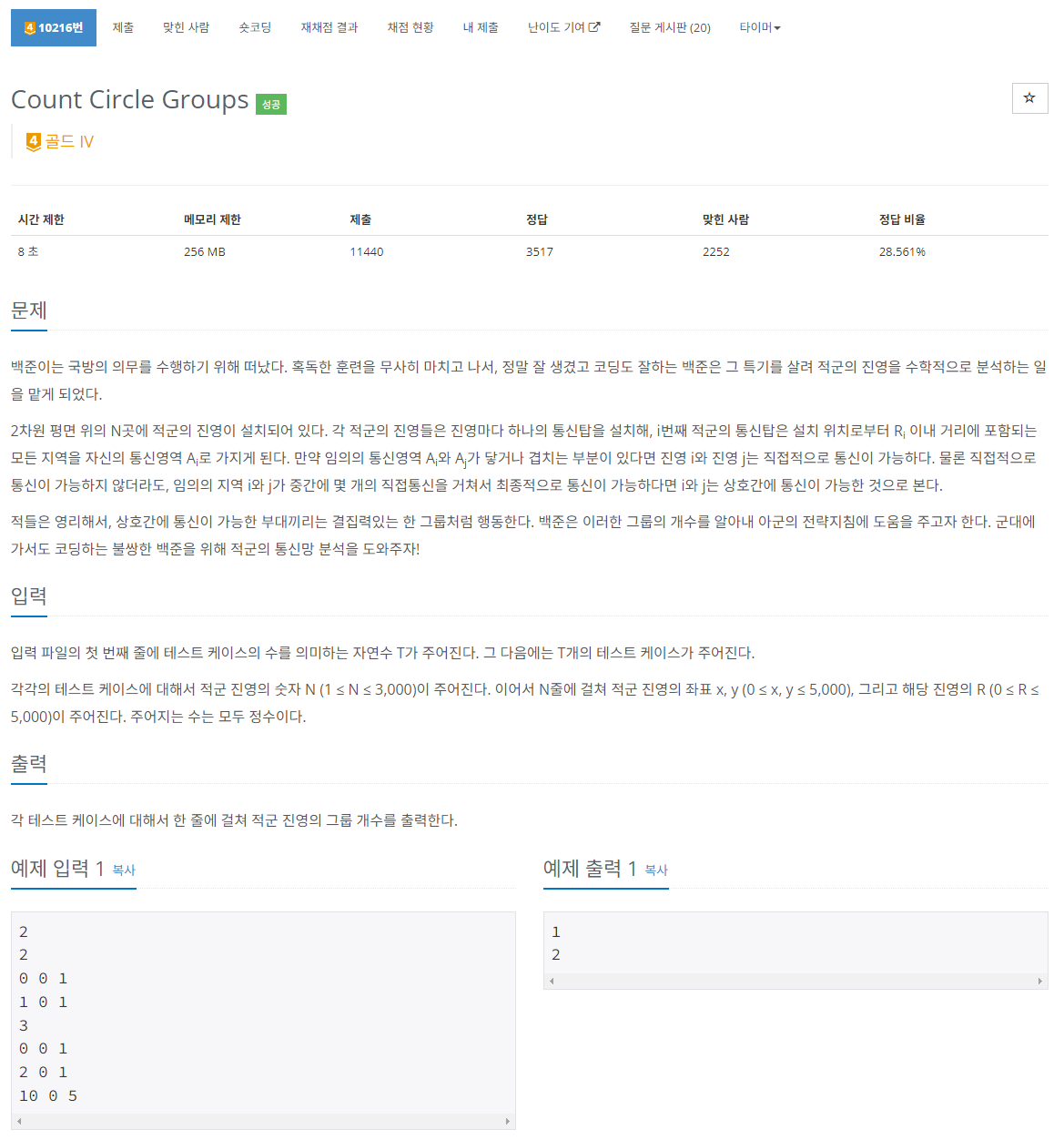
좌표 x,y와 반지름 R이 주어진다. 원이 겹치는 부분끼리 그룹을 지어주고 최종적으로 남은 그룹의 개수를 출력해주면 된다.
float를 최대한 피하는게 좋으므로 거리를 구할때 x1,y1,r1과 x2,y2,r2가 있을 때 (x1-x2)^2+(y1-y2)^2와 (r1+r2)^2를 비교해주면 된다.
#include <iostream>
#include <vector>
#include <tuple>
#include <unordered_set>
using namespace std;
int par[3001];
int find(int x)
{
if (x == par[x]) return x;
par[x] = find(par[x]);
return par[x];
}
void uni(int a,int b)
{
a = find(a);
b = find(b);
if (a < b) par[b] = a;
else par[a] = b;
}
int main()
{
cin.tie(0);
cout.tie(0);
ios_base::sync_with_stdio(0);
int t;
cin >> t;
while (t--)
{
int n,x,y,r,d1,d2,d3;
vector<tuple<int,int,int>> v;
cin >> n;
for (int i = 0; i < n; i++) par[i] = i;
for (int i = 0; i < n; i++)
{
cin >> x >> y >> r;
v.push_back(make_tuple(x, y, r));
for (int j = 0; j < i; j++)
{
d1 = (get<0>(v[i]) - get<0>(v[j])) * (get<0>(v[i]) - get<0>(v[j]));
d2 = (get<1>(v[i]) - get<1>(v[j])) * (get<1>(v[i]) - get<1>(v[j]));
d3 = (get<2>(v[i]) + get<2>(v[j])) * (get<2>(v[i]) + get<2>(v[j]));
if (d1 + d2 <= d3)
{
uni(i, j);
}
}
}
unordered_set<int> uos;
for (int i = 0; i < n; i++) uos.insert(find(i));
cout << uos.size() << "\n";
}
}
12004 Closing the Farm
문제
난이도 : G4
알고리즘 : 분리집합, 그래프 탐색
풀이
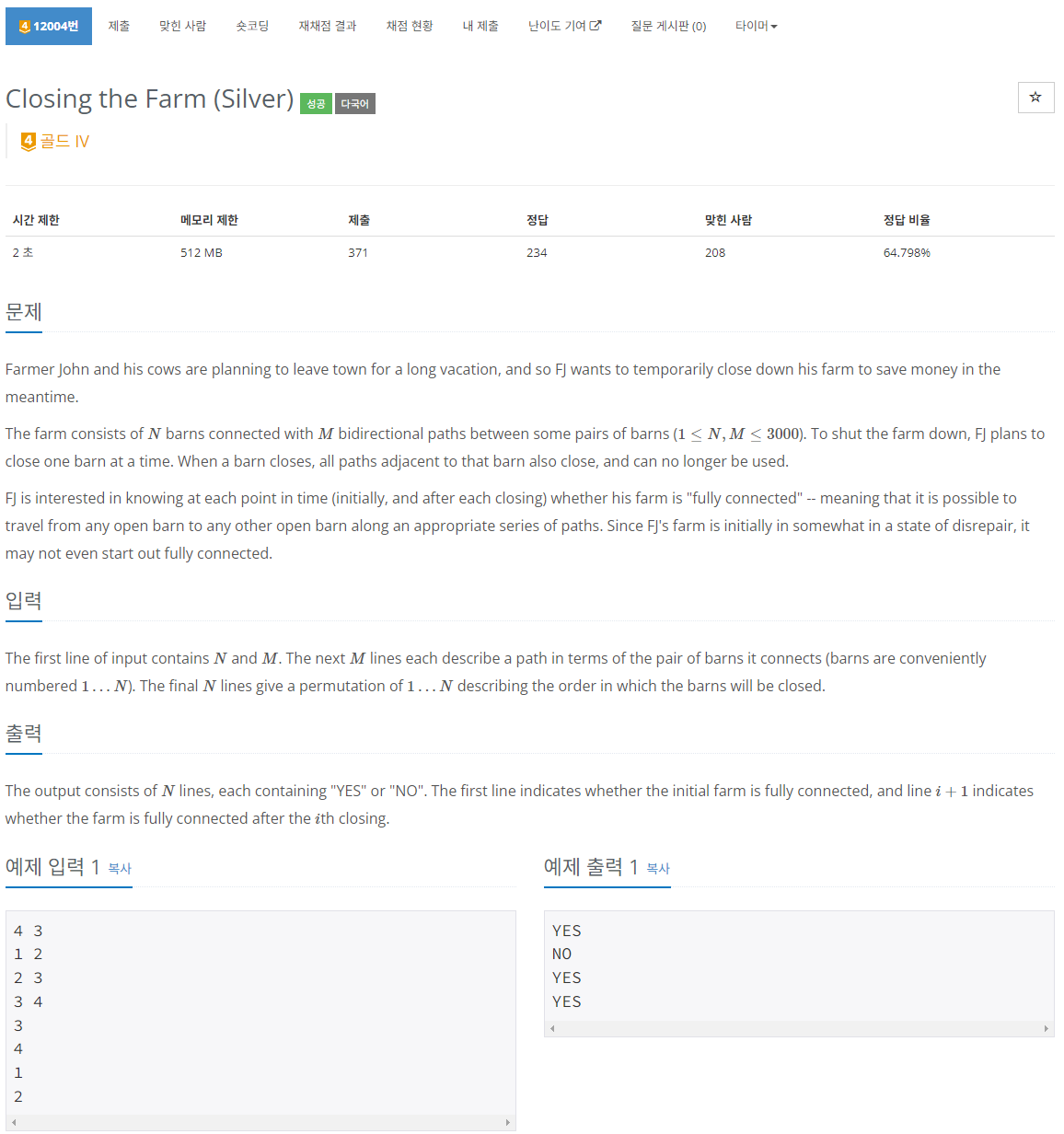
마지막 입력은 중요하지 않다. 초기 상태와 하나씩 지워가면서 다시 분리집합을 구해주면 된다. 굳이 분리집합이 아니어도 다양한 방법으로 풀 수 있다.
#include <iostream>
#include <vector>
#include <unordered_set>
using namespace std;
int par[3001];
int find(int x)
{
if (par[x] == x) return x;
par[x] = find(par[x]);
return par[x];
}
void uni(int a, int b)
{
a = find(a);
b = find(b);
if (a < b) par[b] = a;
else par[a] = b;
}
int main()
{
int n, m, a, b, de=-1;
cin >> n >> m;
vector<pair<int, int>> con;
vector<int> dearr;
pair<int, int> pp;
for (int i = 0; i < m; i++)
{
cin >> a >> b;
con.push_back({ a,b });
}
for (int i = 1; i <= n; i++) par[i] = i;
for (int t = 0; t < n; t++)
{
int le = con.size();
vector<pair<int, int>> ncon;
while (le--)
{
a=con.back().first;
b = con.back().second;
con.pop_back();
pp = {a,b};
if (a != de && b != de)
{
ncon.push_back(pp);
uni(a, b);
}
}
unordered_set<int> uos;
for (int i = 1; i <= n; i++) if (par[i]!=-1) uos.insert(find(i));
while (!ncon.empty())
{
con.push_back(ncon.back());
ncon.pop_back();
}
if (uos.size() != 1) cout << "NO\n";
else cout << "YES\n";
cin >> de;
par[de] = -1;
for (int i = 1; i <= n; i++) if (par[i] != -1) par[i] = i;
}
}'프로그래밍 > 백준' 카테고리의 다른 글
| 백준 9663 NQueen 파이썬으로 다양하게 풀어보기 (0) | 2024.10.02 |
|---|---|
| 백준 20157 - 화살을 쏘자! (파이썬) (0) | 2022.04.28 |
| 백준 1824 - 도미노 (파이썬) (0) | 2022.04.28 |
| 백준 1806 - 부분합 (파이썬) (0) | 2022.03.30 |
| 백준 14267 - 회사 문화 1 (파이썬) (0) | 2022.03.29 |
